强连通分量
定义
强连通的定义是:有向图 G 强连通是指,G 中任意两个结点连通。
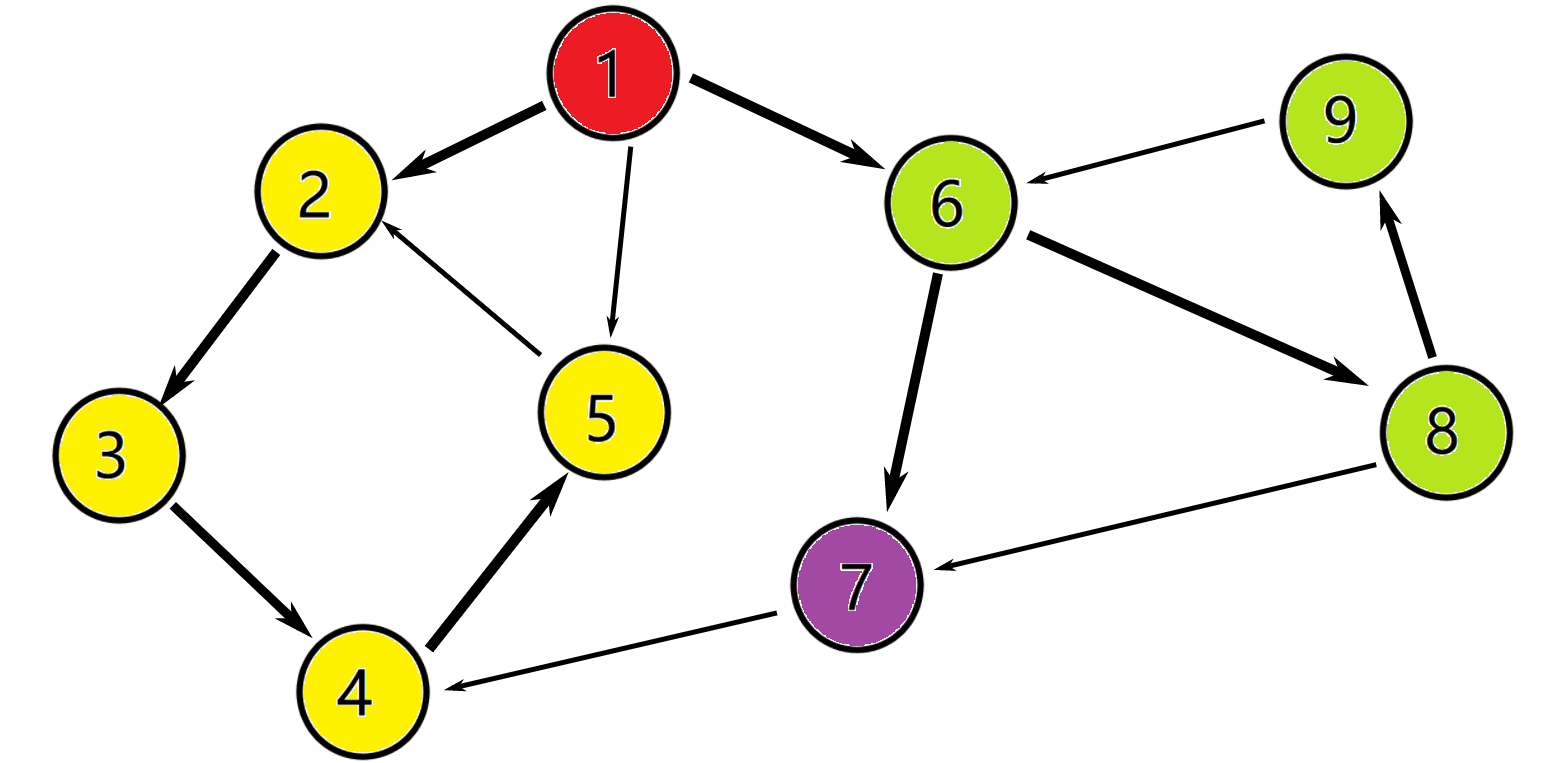
强连通分量(Strongly Connected Components,SCC)的定义是:极大的强连通子图,即彼此两两可达的节点集合。如下图,强连通分量可以表示为[[2, 3, 4, 5], [1], [6, 8, 9], [7]]。
算法
为每个节点维护两个变量:
dfn:该节点被dfs最初访问到的时间low:该节点能够通过其出边回溯到的最小时间
容易得到结论:
- 子树节点的
dfn一定大于当前节点的dfn
- 从根节点开始的一条路径上,
dfn严格递增,low严格非降
算法流程:
按照深度优先搜索算法搜索的次序对图中所有的结点进行搜索,维护每个结点的 dfn 与 low 变量,且让搜索到的结点入栈。每当找到一个强连通元素,就按照该元素包含结点数目让栈中元素出栈。在搜索过程中,对于结点u和与其相邻的结点v(v不是u的父节点)考虑 3 种情况:
- v未被访问:继续对v进行深度搜索。在回溯过程中,用low[v]更新 low[u]。因为存在从u到v的直接路径,所以v能够回溯到的已经在栈中的结点,u也一定能够回溯到。
- v被访问过,已经在栈中:根据 low 值的定义,用low[v]更新low[u] 。
- v被访问过,已不在栈中:说明v已搜索完毕,其所在连通分量已被处理,所以不用对其做操作。
一个连通分量有且仅有一个节点的dfn等于low。该节点一定是在深度遍历的过程中,该连通分量中第一个被访问过的节点,因为它的 dfn 和 low 值最小,不会被该连通分量中的其他结点所影响。因此在回溯的过程中如果dfn == low,说明该节点及栈中节点构成一个SCC。
注意如果原图并非无向连通图,需要在循环内多次调用tarjan,确保每个点都被访问到。
模板
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
|
int time = 1;
Deque<Integer> stk = new ArrayDeque<>();
int[] dfn;
int[] low;
boolean[] inStack;
public List<List<Integer>> tarjan(List<Integer>[] g){
int n = g.length;
dfn = new int[n];
low = new int[n];
inStack = new boolean[n];
List<List<Integer>> ret = new ArrayList<>();
for(int i = 0;i < n;++i) if(dfn[i] == 0) dfs(g, i, ret);
return ret;
}
public void dfs(List<Integer>[] g, int cur, List<List<Integer>> ret){
dfn[cur] = time;
low[cur] = time;
++time;
stk.push(cur);
inStack[cur] = true;
for(int nxt: g[cur]){
if(dfn[nxt] == 0) {
dfs(g, nxt, ret);
low[cur] = Math.min(low[cur], low[nxt]);
}
else if(inStack[nxt]){
low[cur] = Math.min(low[cur], low[nxt]);
}
}
if(low[cur] == dfn[cur]){
List<Integer> ls = new ArrayList<>();
int top = -1;
do{
top = stk.pop();
ls.add(top);
inStack[top] = false;
}while(top != cur);
ret.add(ls);
}
}
|
时间复杂度:O(V+E)
注:Tarjan求强连通分量适用于有向图,无向图的连通分量直接用并查集就行。
题目
802. 找到最终的安全状态 - 力扣(LeetCode)(本题Tarjan并非最优解法)
割点/割边
定义
割点:对于一个无向图,如果把一个点删除后这个图的极大连通分量数增加了,那么这个点就是这个图的割点。
割边:对于一个无向图,如果删掉一条边后图中的连通分量数增加了,则称这条边为桥或者割边。
算法
类似强连通分量。
割点判据有两条:1.根节点且有至少两个子树;2.非根节点且存在一个儿子nxt满足low[nxt] >= dfn[cur]。
割边的判据只有一条:low[nxt] > dfn[cur],说明cur-nxt这条边是割边。
注意当发现已经访问过的节点时,需要用dfn[nxt]更新low[cur],而不是像求解SCC时使用low[nxt]更新。
考虑无向图结构如下,从节点1出发,如果使用的是low[nxt]更新,会导致节点5和节点6的low被更新为1,算法会认为节点5和6不需要经过节点2就能回溯到更早的节点,进而认为节点2不是割点。

也就是说更新low[cur]时不能通过nxt的其它边继续回溯。
模板
适用于无向连通图
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
| int time = 1;
int[] dfn;
int[] low;
List<List<Integer>> edges = new ArrayList<>();
List<Integer> points = new ArrayList<>();
Set<Integer> seenPoint = new HashSet<>();
public void Tarjan(List<Integer>[] g){
int n = g.length;
dfn = new int[n];
low = new int[n];
dfs(g, 0, -1);
}
public void dfs(List<Integer>[] g, int cur, int fa){
dfn[cur] = time;
low[cur] = time;
time++;
int sonCnt = 0;
for(int nxt: g[cur]){
if(nxt == fa) continue;
if(dfn[nxt] == 0){
sonCnt++;
dfs(g, nxt, cur);
low[cur] = Math.min(low[cur], low[nxt]);
if(low[nxt] > dfn[cur]){
List<Integer> edge = new ArrayList<>();
edge.add(cur);
edge.add(nxt);
edges.add(edge);
}
if(seenPoint.contains(cur)) continue;
if(fa != -1 && low[nxt] >= dfn[cur]){
points.add(cur);
seenPoint.add(cur);
}
}
else{
low[cur] = Math.min(low[cur], dfn[nxt]);
}
if(fa == -1 && sonCnt >= 2) points.add(cur);
}
}
|
缩点
定义:把连通分量看成是一个大点,保留那些不在强连通分量里的边,这样的图就是缩点后的图。
缩点后的图保留了所有不在分量里的边,而且对于有向连通图,缩点后的图是一个有向无环图(DAG),可以进行拓扑排序。
题目
1192. 查找集群内的关键连接 - 力扣(LeetCode)----------割边
1489. 找到最小生成树里的关键边和伪关键边 - 力扣(LeetCode)----------割边、缩点
注意本题在缩点后的图中,是可能存在重复边的,因此不能用父节点作为continue的依据,而应该使用来路的那条边作为continue的依据
__END__

