简介

并查集是一种用于处理不相交集合（Disjoint Set）的数据结构，主要用于解决连通性问题。它支持以下两种基本操作：

  1. 查找（Find）：确定一个元素所属的集合。
  2. 合并（Union）：将两个元素所在的集合合并为一个集合。

实现

并查集的核心思想是通过树结构来表示每个集合，每个节点的父节点指向其所在的集合的根节点。判断两个节点是否同属一个集合通过判断根节点是否相同实现。合并两个节点通过将一个节点的根节点赋值为另一个根节点的父亲来实现。

通过路径压缩和按秩合并，可以显著提高算法的效率。

  1. 路径压缩（Path Compression）
    在查找过程中，将路径上的所有节点直接连接到根节点，从而减少后续查找的深度。路径压缩可以将单次查找的复杂度降低到接近常数时间。
  2. 按秩合并（Union by Rank）
    秩即树的深度，在合并两个集合时，总是将秩较小的树合并到秩较大的树下。这样可以防止树变得过高，从而保证查找和合并操作的高效性。

代码模板

为了简化实现，代码中的rank数组实际上并不是树的深度，而是树的节点数量，因此严格来说应该叫启发式合并，与按秩合并的效果是类似的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class UnionFind {
    int n;
    int[] rank;
    int[] fa;

    UnionFind(int _n){
        this.n = _n;
        this.rank = new int[n];
        this.fa = new int[n];
        for(int i = 0;i < n;++i){
            rank[i] = 1;
            fa[i] = i;
        }
    }

    public int findFa(int x){
        return fa[x] == x ? x : (fa[x] = findFa(fa[x]));
    }

    public void union(int x, int y){
        x = findFa(x);
        y = findFa(y);
        if(x == y) return;
        if(rank[x] < rank[y]){
            int tmp = x;
            x = y;
            y = tmp;
        }
        fa[y] = x;
        rank[x] += rank[y];
    }

    public boolean isConnected(int x, int y){
        x = findFa(x);
        y = findFa(y);
        return x == y;
    }
}

复杂度分析

路径压缩：单次查找操作的复杂度接近 O(α(n))，其中 α(n) 是阿克曼函数的反函数，增长非常缓慢，可以认为是常数级别。

按秩合并：在路径压缩的基础上，按秩合并可以进一步优化合并操作的复杂度。

如果并查集仅使用路径压缩，不使用按秩合并，单次查询的复杂度最坏会达到O(logn)

例如下图这种情况：

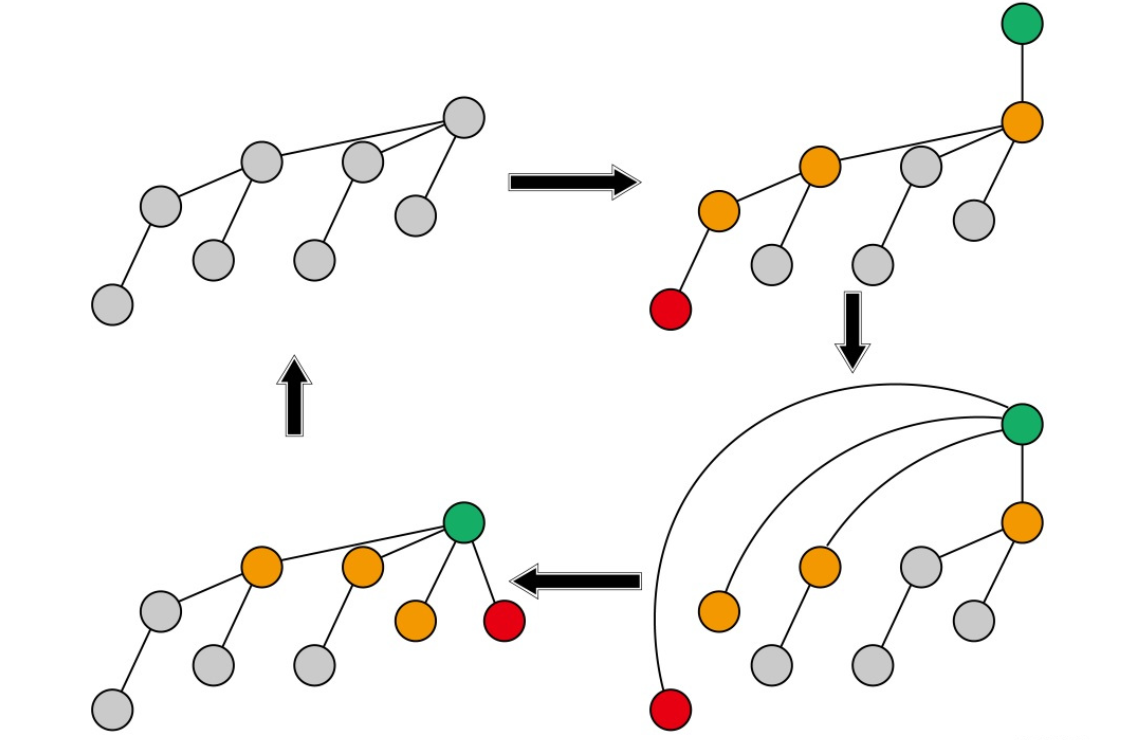
image-20231021193621956

初始状态为左上图，第一次合并大的集合和绿色这个点，之后查询红点，红点路径的长度为 O(log(n)) ，所以查询一次的复杂度为O(log(n)) ,而路径压缩之后整棵树又变成类似左上图的结构，如果再一次和一个绿点合并之后再查询红点，复杂度还是O(log(n)) 的，这就导致产生一个循环，用这样的合并和查询就可能导致不按秩合并的并查集的复杂度降到O(nlog(n)) 。

__END__