SkipList

简介

前面介绍的ZipList和QuickList在首尾的操作效率很高，为O(1)，但查找元素时只能顺次遍历，导致随机查找的效率不高，可以认为导致这个问题的原因是链表元素间的跨度太小。为了解决这个问题，SkipList在有序链表的基础上增加了多层索引，使得查找的时间复杂度从O(n)降低到平均 O(logn)。

跳表的介绍和简易java实现可以参见之前的文章：跳表简介及简单实现

具体实现

概述

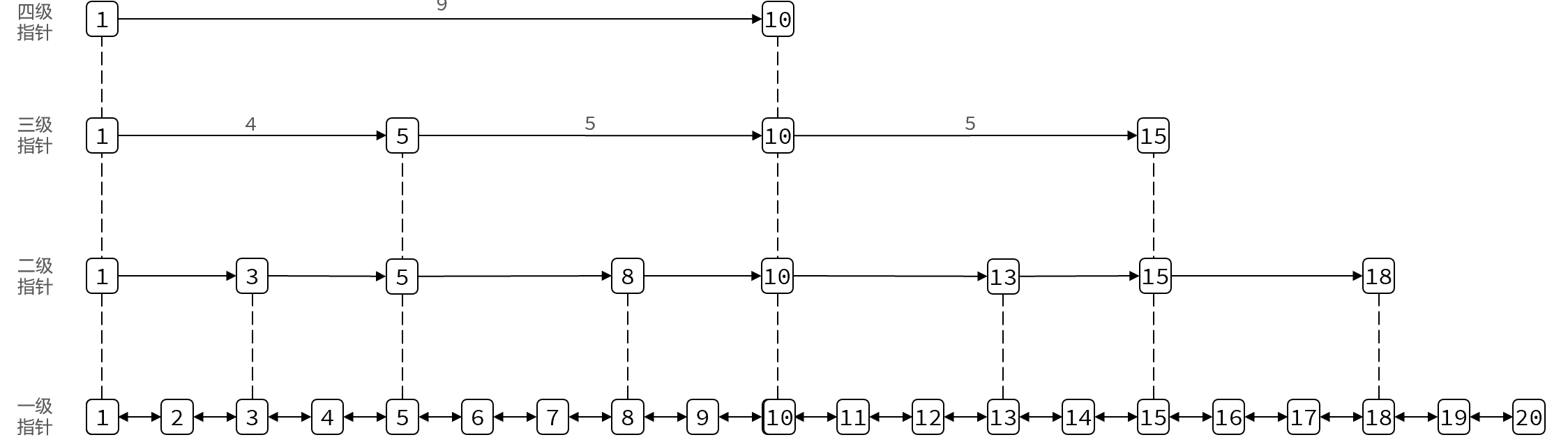
SkipList的元素按照升序存储，且每个节点可能包含多个指针，指针从底层到顶层的跨度逐渐增加，示意图如下：

image-20250220143647198

结构体定义代码如下：

1
2
3
4
5
6
7
8
9
// t_zset.c
typedef struct zskiplist {
    // 头尾节点指针
    struct zskiplistNode *header, *tail;
    // 节点数量
    unsigned long length;
    // 最大的索引层级，默认是1
    int level;
} zskiplist;
1
2
3
4
5
6
7
8
9
10
// t_zset.c
typedef struct zskiplistNode {
    sds ele; // 节点存储的值
    double score;// 节点分数，排序、查找用
    struct zskiplistNode *backward; // 前一个节点指针
    struct zskiplistLevel {
        struct zskiplistNode *forward; // 下一个节点指针
        unsigned long span; // 索引跨度
    } level[]; // 多级索引数组
} zskiplistNode;

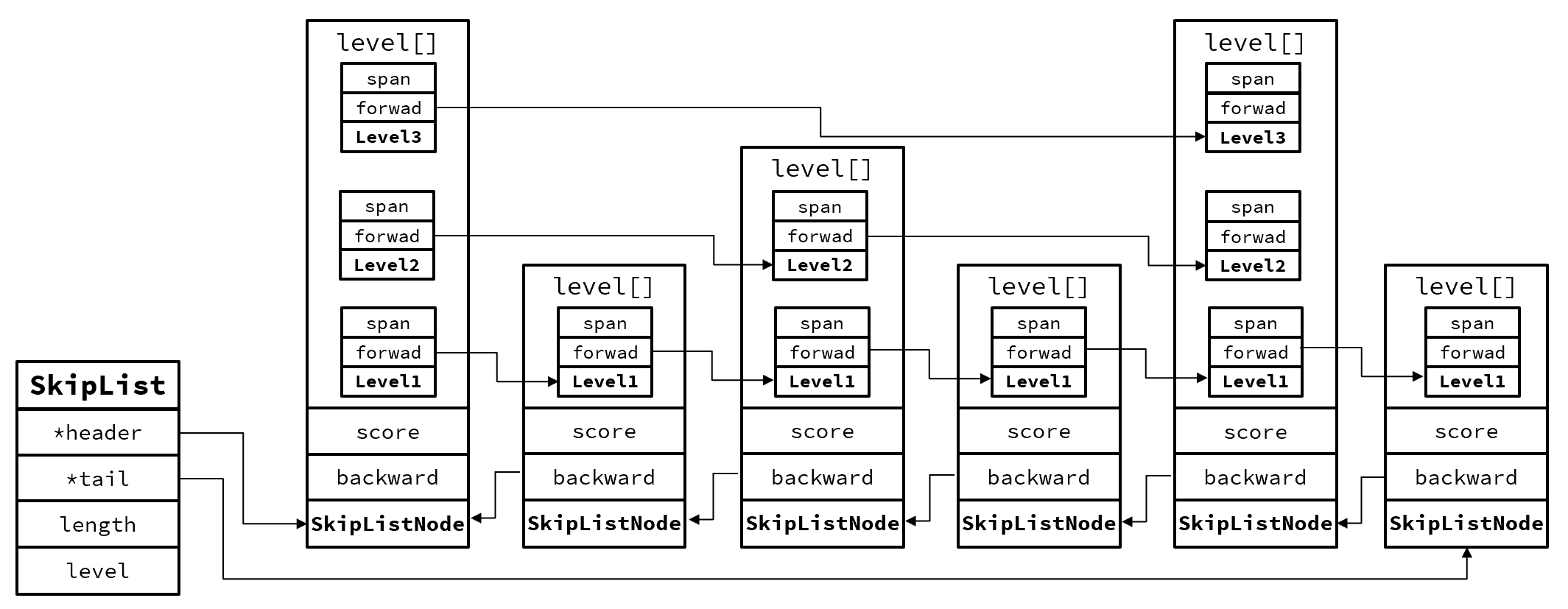
image-20250220144412629

与简易实现作对比可以发现，在 SkipList中，除了用于快速查找、插入和删除操作的多层前向指针外，还存在一个 backward 指针。在某些场景下，需要对有序集合进行反向遍历，例如排行榜逆序展示，这时 backward 指针就发挥了重要作用。

复杂度分析
  • 时间复杂度：跳表的查找、插入和删除操作的平均时间复杂度都是 O（logn），这是因为随机层高的设计使得跳表在大多数情况下能够快速地跳过一些不必要的节点。详细证明参见论文《Skip Lists: A Probabilistic Alternative to Balanced Trees》。
  • 空间复杂度：跳跃表的空间复杂度是O(n)，扩展层数的概率p越大，所需的空间开销（n前面的常数）就越大。
跳表与平衡树、哈希表的比较
  • skiplist和各种平衡树（如AVL、红黑树等）的元素是有序排列的，而哈希表不是有序的。因此，在哈希表上只能做单个key的查找，不适宜做范围查找。所谓范围查找，指的是查找那些大小在指定的两个值之间的所有节点。
  • 在做范围查找的时候，平衡树比skiplist操作要复杂。在平衡树上，我们找到指定范围的小值之后，还需要以中序遍历的顺序继续寻找其它不超过大值的节点。如果不对平衡树进行一定的改造，这里的中序遍历并不容易实现。而在skiplist上进行范围查找就非常简单，只需要在找到小值之后，对第1层链表进行若干步的遍历就可以实现。
  • 平衡树的插入和删除操作可能引发子树的调整，逻辑复杂，而skiplist的插入和删除只需要修改相邻节点的指针，操作简单又快速。
  • 从内存占用上来说，skiplist比平衡树更灵活一些。一般来说，平衡树每个节点包含2个指针（分别指向左右子树），而skiplist每个节点包含的指针数目平均为1/(1-p)，具体取决于参数p的大小。如果像Redis里的实现一样，取p=1/4，那么平均每个节点包含1.33个指针，比平衡树更有优势。
  • 查找单个key，skiplist和平衡树的时间复杂度都为O(log n)，大体相当；而哈希表在保持较低的哈希值冲突概率的前提下，查找时间复杂度接近O(1)，性能更高一些。
  • 从算法实现难度上来比较，skiplist比平衡树要简单得多。
Redis为什么用跳表而不是平衡树？

除了以上分析的原因外，Redis的作者 @antirez 原回答如下：

There are a few reasons:

  1. They are not very memory intensive. It’s up to you basically. Changing parameters about the probability of a node to have a given number of levels will make then less memory intensive than btrees.
  2. A sorted set is often target of many ZRANGE or ZREVRANGE operations, that is, traversing the skip list as a linked list. With this operation the cache locality of skip lists is at least as good as with other kind of balanced trees.
  3. They are simpler to implement, debug, and so forth. For instance thanks to the skip list simplicity I received a patch (already in Redis master) with augmented skip lists implementing ZRANK in O(log(N)). It required little changes to the code.

第一条从内存角度说明，因为其内存占用的常数不大且可以根据概率p调整；

第二条从遍历操作说明，其局部性较优；

第三条单纯从实现难度说明。

__END__